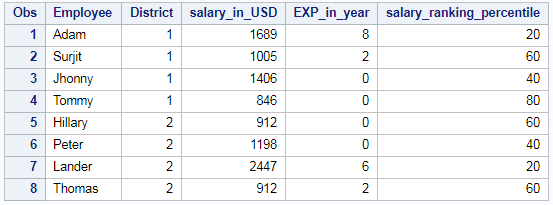Ranking of column in SAS – PROC RANK

In this Tutorial we have explained on different ways of Ranking of column in SAS using PROC RANK Statement. In order to Rank column in SAS we use PROC RANK Statement. Different scenario which we use PROC RANK statement is shown below. These Scenarios include Percentile Rank, Quartile Rank and Decile Rank of column in SAS

• Rank of a column in SAS – PROC RANK
• Rank of column in Ascending order in SAS
• Rank of All the numeric column in SAS
• Rank of a column by Group – GroupBy Rank in SAS
• Rank More than one column in SAS
• Rank , Mean Rank , Dense Rank in SAS
• Percentile Rank, Quartile Rank and Decile Rank of the column in SAS

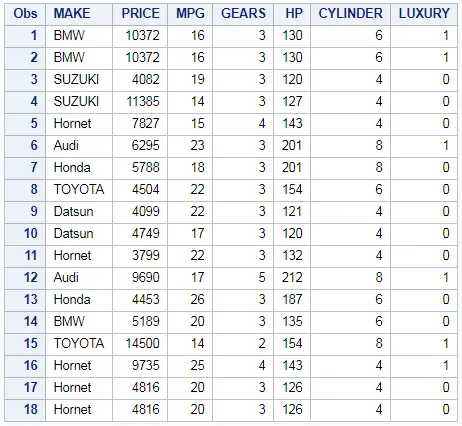
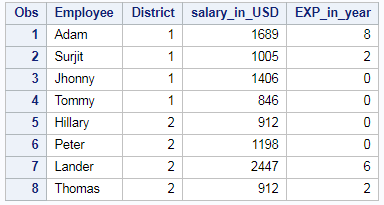
So we will be using EMP_DET Table in our example

Rank of a column in SAS – PROC RANK

Rank of the column in descending order in SAS using PROC RANK is shown below. Rank of the “salary_in_USD” column is calculated

/* rank of a column */

proc rank data=EMP_DET out=results ties=low descending; 
var salary_in_USD; 
ranks salary_ranking; 
run; 

So the Resultant table will be

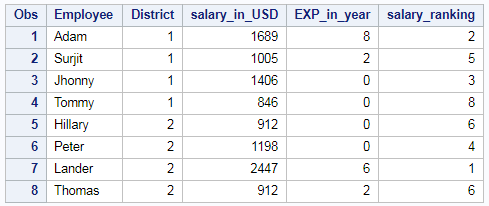
Rank of column in Ascending order in SAS

Rank of the column in Ascending order in SAS using PROC RANK is shown below. Rank of the “salary_in_USD” column in ascending order is calculated

 /* rank of a column in ascending */ 

proc rank data=EMP_DET out=results ties=low; 
var salary_in_USD; 
ranks salary_ranking; 
run;

So the resultant table will be

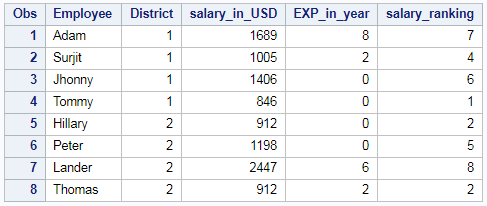
Rank of All the numeric column in SAS

Rank of all the numeric column in descending order in SAS using PROC RANK is shown below. Rank of the entire numeric column is calculated

 /* rank of all numeric column */ 

proc rank data=EMP_DET out=results ties=dense descending; 

So the resultant table will be

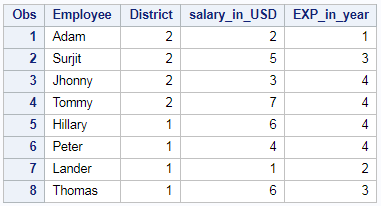
Rank of a column by Group – GroupBy Rank in SAS

Rank of the column by Group in descending order using PROC RANK is shown below. Rank of the “salary_in_USD” column by “District” group is shown below.

 /* rank of a column by group*/ 

proc rank data=EMP_DET out=results ties=low descending; 
by District; 
var salary_in_USD; 
ranks salary_ranking_grp; 
run;

So the resultant table will be

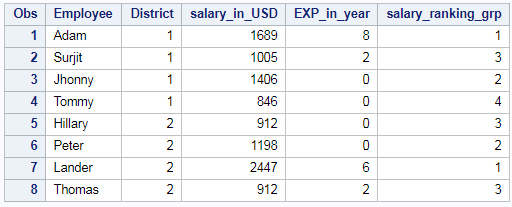
Rank more than one column in SAS

Rank of more than one column in SAS by descending order using PROC RANK is shown below. Rank of the “salary_in_USD” column and “EXP_in_year” column is calculated separately

 /* rank of more than one column */ 

proc rank data=EMP_DET out=results ties=low descending; 
var salary_in_USD EXP_in_year; 
ranks salary_ranking Exp_ranking; 
run;

So the resultant table will be

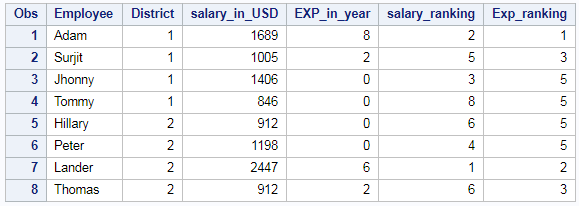
Rank of the column in case of Tie – High

Rank of the column in descending order using PROC RANK is shown below.  In case of Tie we will be using highest Rank of the “salary_in_USD” column is shown below.

 /* rank of a column - high*/ 

proc rank data=EMP_DET out=results ties=high descending; 
var salary_in_USD; 
ranks salary_ranking; 
run;  

When there is a tie in Ranking, Highest ranking is given to both the values and one rank is skipped. Here 6^th rank was skipped and 7^th rank (highest rank) is given to both the values on tie. So the resultant table will be

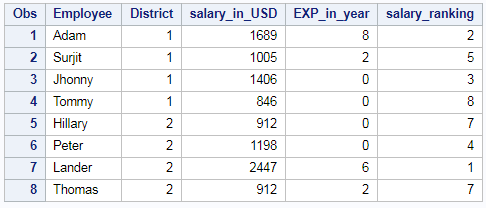
Rank of the column in case of Tie – Dense

Rank of the column in descending order using PROC RANK is shown below.  In case of Tie we will be using Dense Rank of the “salary_in_USD” column is shown below.

 /* rank of a column - dense*/ 

proc rank data=EMP_DET out=results ties=dense descending; 
var salary_in_USD; 
ranks salary_ranking; 
run;

When there is a tie in Ranking, Dense ranking is given to both the values i.e. rank is not skipped. Here 6^th rank (Dense rank) is given to both the values on tie. So the resultant table will be

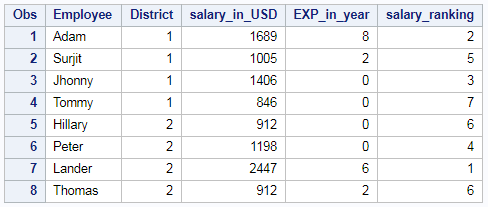
Rank of the column in case of Tie – Mean

Rank of the column in descending order using PROC RANK is shown below.  In case of Tie we will be using Mean Rank of the “salary_in_USD” column is shown below.

/* rank of a column - mean*/ 

proc rank data=EMP_DET out=results ties=mean descending; 
var salary_in_USD; 
ranks salary_ranking; 
run;  

When there is a tie in Ranking, Mean ranking is given to both the values and one rank is skipped. Here rank 6.5 (Mean of 6 and 7 is 6.5) was given to both the values on tie by skipping 6^th and 7^th rank. So the resultant table will be

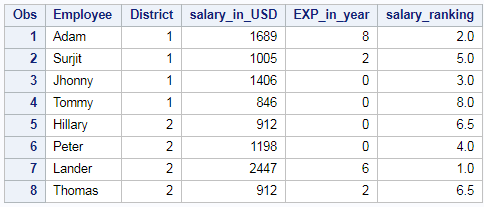
Rank of the column – Quartile:

Rank of the column in Quartile using PROC RANK is shown below.  We will be ranking “salary_in_USD” column in quartiles i.e (0,1,2,3) is shown below.

/* rank of a column _ quartile*/ 

proc rank data=EMP_DET out=results ties=low descending groups=4; 
var salary_in_USD; 
ranks salary_ranking_quartile; 
run;

So the resultant table will be grouped under 4 ranks

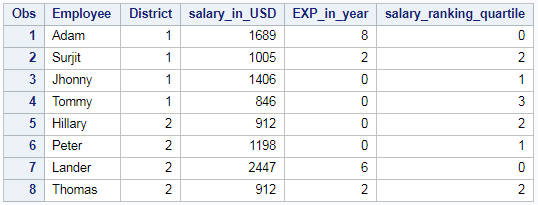
Rank of the column by Group – Quartile:

Rank of the column in Quartile using PROC RANK is shown below.  We will be ranking “salary_in_USD” column in quartiles by “District” groups as shown below.

/* rank of a column by group - Quartile */ 

proc rank data=EMP_DET out=results ties=low descending groups=4; 
by District; 
var salary_in_USD; 
ranks salary_ranking_quartile; 
run;

So the resultant quartile ranks which is ranked by “district” group will be

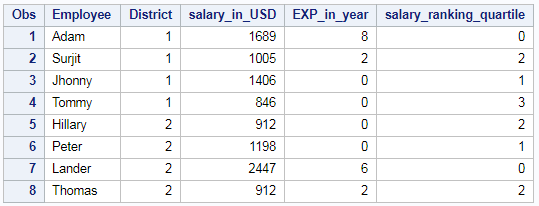
Rank of the column – Percentile:

Rank of the column in Percentile using PROC RANK is shown below.  We will be ranking “salary_in_USD” column in percentiles i.e (1-100) is shown below.

/* rank of a column - percentile*/ 

proc rank data=EMP_DET out=results ties=low descending groups=100; 
var salary_in_USD; 
ranks salary_ranking_percentile; 
run; 

So the resultant table will be grouped under 100 ranks

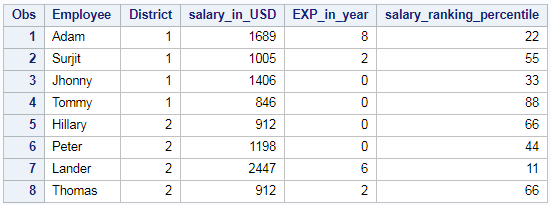
Rank of the column by Group – Percentile:

Rank of the column in Percentile using PROC RANK is shown below.  We will be ranking “salary_in_USD” column in percentiles i.e (1-100) is shown below. We will be ranking this column based on “district” groups

/* rank of a column by group - percentile */ 

proc rank data=EMP_DET out=results ties=low descending groups=100; 
by District; 
var salary_in_USD; 
ranks salary_ranking_percentile; 
run;

So the resultant percentile ranks which is ranked by “district” group will be