Summary or Descriptive statistics in SAS

Summary or Descriptive statistics in SAS is obtained using multiple ways like PROC Means and PROC Univariate. Summary statistic of all columns in SAS. Descriptive or Summary statistics of single column in SAS. Let’s see an example of each

• Summary or Descriptive statistics of single column in SAS: PROC MEANS
• Summary or Descriptive statistics of a column by Groups in SAS : PROC MEANS
• Summary or Descriptive statistics of multiple columns in SAS: PROC MEANS
• Summary or Descriptive statistics of column by group in SAS: PROC UNIVARIATE
• Summary or Descriptive statistics of single column in SAS: PROC UNIVARIATE
• Summary or Descriptive statistics of all columns in SAS: PROC FREQ

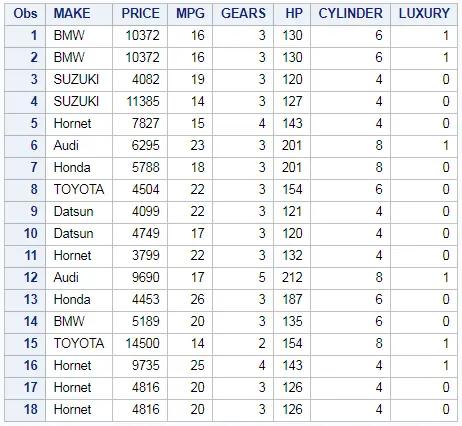
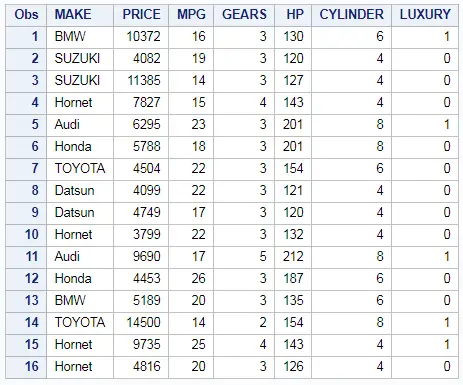
We will be using the table name CARS.

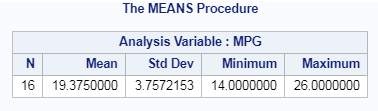
Summary or Descriptive statistics of single column in SAS: PROC MEANS

Summary or Descriptive statistics of single column in SAS using PROC MEANS

/* SUMMARY statistics of one var by proc means */ 

PROC MEANS DATA=cars; 
   VAR MPG; 
RUN;

Summary or Descriptive statistics of a column by Groups in SAS : PROC MEANS

Summary or Descriptive statistics of a column(MPG) by Groups(Luxury) in SAS using PROC MEANS. CLASS statement is used to define groups.

PROC MEANS DATA=cars; 
   VAR MPG; 
   CLASS LUXURY; 
RUN; 

Summary or Descriptive statistics of multiple columns in SAS: PROC MEANS

Summary or Descriptive statistics of multiple columns (MPG, GEAR and HP) in SAS using PROC MEANS is accomplished using VAR statement as shown below.

/* SUMMARY statistics of more than one var by proc means */ 

PROC MEANS DATA =cars; 
   VAR MPG GEARS HP; 
RUN; 

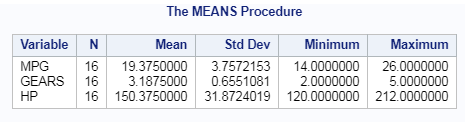
Summary or Descriptive statistics of multiple columns by Groups in SAS: PROC MEANS

Summary or Descriptive statistics of multiple columns (MPG, GEAR and HP) by Group (Luxury) in SAS using PROC MEANS is accomplished using VAR statement and CLASS statement as shown below.

PROC MEANS DATA=cars; 
    VAR MPG GEARS HP; 
	CLASS LUXURY; 
RUN; 

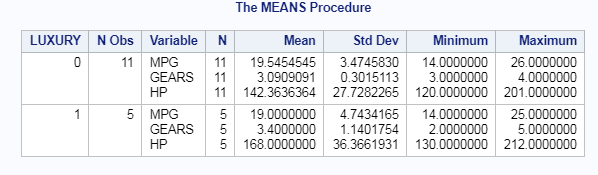
Summary or Descriptive statistics of single column in SAS: PROC UNIVARIATE

Summary or Descriptive statistics of single column (HP) in SAS using PROC UNIVARIATE is accomplished using VAR statement as shown below.

/* PROC UNIVARIATE OF SINGLE COLUMN */ 

PROC univariate data=cars; 
   VAR HP; 
RUN; 

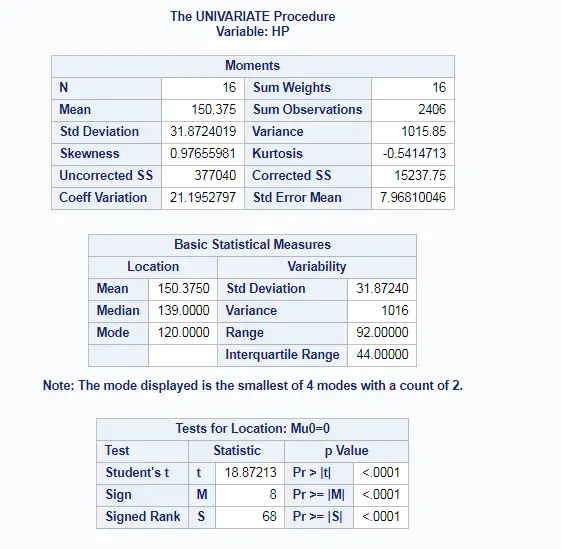
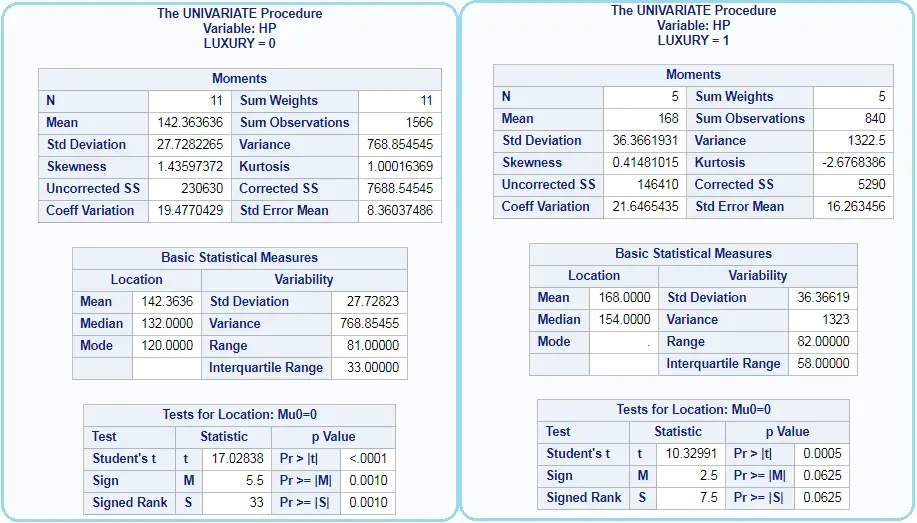
Summary or Descriptive statistics of column by group in SAS: PROC UNIVARIATE

Summary or Descriptive statistics of single column (HP) by group (LUXURY) in SAS using PROC UNIVARIATE is accomplished using VAR statement and CLASS Statement as shown below.

PROC univariate data=cars; 
   VAR HP; 
   class LUXURY; 
RUN; 

Summary or Descriptive statistics of multiple column in SAS: PROC UNIVARIATE

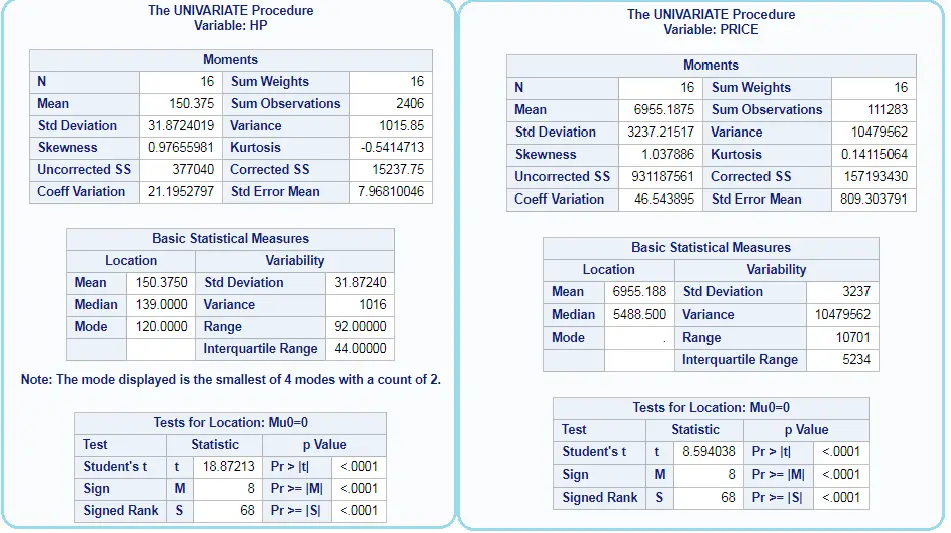
Summary or Descriptive statistics of multiple column (HP, PRICE) in SAS using PROC UNIVARIATE is accomplished using VAR statement as shown below.

/* PROC UNIVARIATE OF MORE THAN ONE COLUMN */ 

PROC univariate data=cars; 
   VAR HP PRICE; 
RUN;

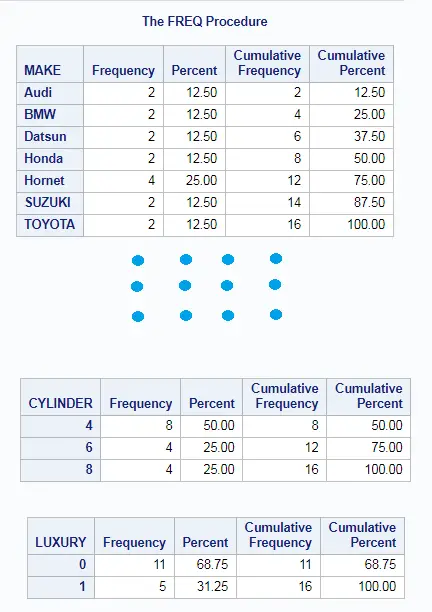
Summary or Descriptive statistics of all columns in SAS: PROC FREQ

Summary or Descriptive statistics of all in SAS using PROC FREQ  is accomplished using table statement with _ALL_  as shown below.

/* proc freq of all the column*/ 

proc freq data=cars; 
table _ALL_; 
run;

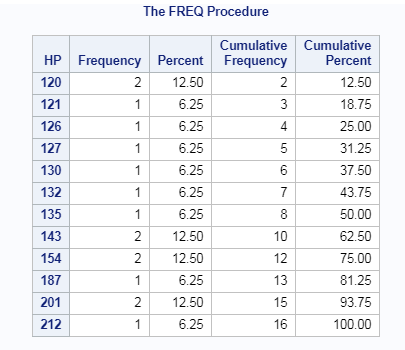
Summary or Descriptive statistics of single column in SAS: PROC FREQ

Summary or Descriptive statistics of single column(HP) in SAS using PROC FREQ  is accomplished using table statement as shown below.

/* proc freq of single the column*/ 

proc freq data=cars; 
table HP; 
run;